Welcome To Quadratics!
Grade 10 Math
First, What is a Parabola?
A Parabola is any line that is curved.
Some Real Life examples include:
- McDonalds Logo
- Eiffel Tower Base arch
- Roller Coaster
- Shooting Basketball
Requirements
Vertex Form
Learning Goals For this Unit: Vertex Form
- Transform y=x^2 for a given quadratic relation
- Graph using the vertex form of a quadratic relation
Vertex Form Unit Summary
Vertex Form is finding the vertex of a parabola that has the minimum or max value on a graph
The purpose of Vertex form is:
- If a Parabola is stretched
- If the Parabola is opened in the direction of up or down
- To identify the X value in a vertex
- To identify the Y Value in a vertex
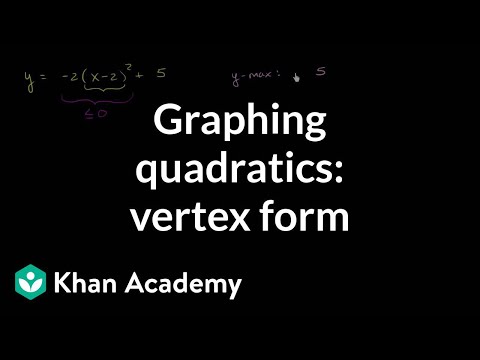
- The formula for the Vertex form in a Parabola is Y=a(x-h)^2+k
- The a value in y=a(x-h)^2+k tells you the direction of the parabola opening either up or down.
- *If a is greater than 0 the direction of opening will open up, if a is less than 0 the direction of opening is down.
- Also if the a variable is positive ,the parabola direction of opening is up
- if the a value of the parabola is negative, the parabola direction of opening is down.
- The (h,k) variables represent the vertex in a Parabola
- The H is the x coordinate of the vertex and k being the y coordinate of the vertex.
- When the Parabola is opening up ,the vertex shows a minimum value, when the parabola is opening down, the vertex has a maximum value.
- Variables that will change the Parabola's shape:
'h' will move the parabola right or left being horizontal translation
'k' will move the parabola up or down being a vertical translation
Graph of Vertex Form
Explanation of the Graph
Vertex Form equation given above: y=(x-3)^2+2
The vertex in this equation y=(x-3)^2+2 is (3,2)
(h,k)
The H is the x coordinate of the vertex and k being the y coordinate of the vertex.
- The h value becomes the opposite, in this equation the value of h was negative 3 ,when changed it becomes positive 3.
- The Direction of opening for this Parabola is up.
- The Parabola's vertex has a minimum value since the direction of opening is down, in this case the lowest value the parabola reaches is 3.
Word Problems: Vertex Form
A football is kicked into the air. Its height in meters after t seconds is given by h=-4.9(t-2.4)^2+29
What was the height of the football when it was kicked?
t=0
h=-4.9(t-2.4)^2+29
h=-4.9(0-2.4)^2+29
h=-4.9(-2.4)^2+29
h=-4.9(5.76)+29
h=-28.224+29
h=0.77
Therefore 0.77m was the football when it was kicked.
What was the maximum height of the ball?
Using the vertex, the maximum height of the ball is 29 m after 2.4 seconds
How high was the ball after 2s?
t=2
h=-4.9(t-2.4)^2+29
h=-4.9(2-2.4)^2+29
h=-4.9(-0.4)^2+29
h=-4.9(-0.16)+29
h=-0.784+29
h=28.2
The ball reached a height of 28.2 m after 2 seconds
Was the ball still in the air after 5s?
t=5
h=-4.9(t-2.4)^2+29
h=-4.9(5-2.4)^2+29
h=-4.9(2.6)^2+29
h=-4.9(6.76)+29
h=-33.124+29
h=-4.124
No the ball was not in the air after 5 seconds.
Resources
Factored Form
Learning Goals
- Be able to solve Quadratics in Factored Form
- Be able to graph a quadratic equation in Factored Form
Factored Form Unit Summary
- The equation for Factored Form is represented as y=a(x-s)(x-t)
- The equation tells the zeros or the roots
- The equation also tells the x-intercepts x=s,x=t
- If a>0, the Parabola opens upwards
- If a<0, The parabola opens downwards
- when using factored form we use FOIL which stands for First Outside Inside Last to check if our factors for the terms are correct
a>0
- If a>0, the Parabola opens upwards
a<0
- If a<0, The parabola opens downwards
FOIL
Outside
Inside
Last
Different Forms of Factoring
- Common Factoring
- Factoring by Grouping
- a=1
- a≠1
- Difference of Squares
- Factoring Perfect Squares
Common Factoring
- To apply Common Factoring you must find the GCF (Greatest Common Factor) in all the terms in the expression. Keep in mind that the numbers and variables must make each term when you expand and simplify it.
- After write the common factor in front of the bracket that you divided with all the terms. INSIDE the brackets put the reduced terms that were divided by the common factor.
Common Factoring Example:
Factor 16xy2 + 20x2y – 4x3y2
- Find GCF of the terms
16xy2+20x2y-4x3y2
Each of these terms can be divided by 4 evenly
2. The variables xy^2, x^2y and x^3y^2 have xy in common
3. Therefore the common factor would be 4xy
4. 4xy(4y+5x-x2 ) is the final answer
Factoring By Grouping
- To use Factor by Grouping we have to see if any of the four terms have anything in common or called GCF. If there is anything in common, factor it out.
- Then we create smaller groups by grouping the two terms separately
- Next we factor the GCF's from each binomial term
- While factoring the GCF we must reduce the terms inside the parenthesis by using the GCF from the term it was divided from.
- Make sure that the GCF is divided evenly with the terms inside the parenthesis and make the signs are correct
- See if any of the factors can be reduced to its simplest.
Factoring by Grouping Example:
- x^3-5x^2+3x-15
- Create smaller groups
- x^3-5x^2+3x-15
- Take GCF's out of the Binomials, in this case its x^2 and 3
- x^2(x-5)+3(x-5)
- See if it can be reduced even more, in this case it cannot reduced even more
- (x-5)(x^2+3)
A=1
- In this type of factoring we use the quadratic formula known as ax^2+bx+c .
- Then we write the factors of C
- Identify which pair of factors add up to to get the middle term or variable b
- Substitute the factors inside the two binomials
A=1 Example
ax^2+bx+c
Now we identify the factors of c being 4
1x4=4
now to verify to see if it will add to get the middle term being 5x
1x+4x=5x
yes it does work
Finally we see if we can reduce it however we can't anymore because its at its simplest.
A≠1
- We again use the quadratic formula being ax^2+bx+c
- After we multiply the a variable and the c variable together to get the product
- After we get the product we determine what factors ac add to get the b variable or the middle term
- Then we brake the middle term into the two factors of the product
- After remove common factors
- Then finally group into two binomials
A≠1 Example
axc=(3)(4)=12
3x^2+3x+4x+4
Now we group the expression into two binomials
(3x^2+3x)+(4x+4)
Now we remove the common factors being 3x and 4
3x(x+1)+4(x+1)
Now we put the common factors together and leave the other binomial bracket.
(3x+4)(x+1)
Difference of Squares
In this equation the b values have opposite signs making the b values cancel out only when they are being added to get the middle term. Therefore making the equation have no middle term.
Difference of Squares Example
As you can see there is no middle term so we have - and a + that way when we add the opposite integers they cancel out.
X^2-36
(x-6)(x+6)
as you can see we had to choose the square root of 36 which is 6. and make 6 negative and positive.
Factoring a Perfect Square
(X-2)^2= (x-2)(x-2)
Factoring a Perfect Square Example
x^2+3x+3x+9+
x^2+6x+9x
This is a perfect square Trinomial
Word Problems Factored Form
The area of a square is numerically equal to twice its perimeter. Find the length of a side of the square.
s^2=2(4s)
s^2+8s
s^2-8s=0
Now we factor out the s since its common
s(s-8)=0
s-8=0
s=8
The length of the side is 8.
Graphing Factored Form
Standard Form
I will be able to:
- Find direction of opening, axis of symmetry,vertex,the zeros,and y-intercept given to me for a quadratic relationship given in standard form
- Find the zeros in a quadratic relationship by using the quadratic formula
- Being able to graph the quadratic relation given to me in standard form
- Find the zeros,vertex and y-intercept in application problems
Standard Form Unit Summary
To find the zeros or
x-intercepts
we use the quadratic formulaThe Quadratic Formula is :
x=b±√b^2-4(a)(c)/2(a)
The Discriminant is: √b^2-4ac The terms under the square root
To find the vertex we the take the two x-intercepts and add them then divide the number added by 2.
*The y-Intercept is already in the standard form equation
Completing the Square is taking the Standard Form equation and changing it into a(x+d)^2+e=0
In Word Problems when they say:
- Find the distance the ball flew you will have to find the x-intercepts also known as the zeros
- Find the Max height you will have to use completing the square
Quadratic Formula
x=b±√b^2-4(a)(c)/2(a)
For Example
PART 1:
y=x^2-2x-8
ax^2+bx+c=0
x=-b±√b^2-4(a)(c)/2(a)
x=-(-2)±√(-2)^2-4(1)(-8)/2(1)
x=2±√4+32/2
x=2±√36/2
x=2+6/2
x=8/2
x=4
PART 2:
As you can see this is 1 X-intercept or 1 zero now we have to find the other x intercept
:
So we take the result of the discriminant:
x=2+6/2
But we flip the operation, so in this case instead of the numbers being added it will be subtracted
x=2-6/2
x=-4/2
x=-2 NOT VALID
Therefore the zeros or x-intercepts are:
(4,0) (-2,0)
(x,y) (x,y)
To get the vertex we add X1+X2/2.This gives us the axis of symmetry
4+(-2)/2
2/2
=1
The Axis of Symmetry is 1
Now we sub in the 1 into our standard form equation
y=x^2-2x-8
y=(1)^2-2(1)-8
y=1-2-8
y=-9
The Vertex is -9
If the Discriminant is:
- D<0: If the Discriminant is less than 0, There's going to be no solution because the Discriminant is going to be negative.
- D>0: If the
Discriminant
is greater than zero there will be two solutions or x-Intercepts. - D=0: If the
Discriminant
equals 0 there will be only one solution or in other words one x-intercept.
Completing The Square
We have to have a standard form equation:
ax^2+bx+c
x^2+12x+20
Now we just place a bracket around the binomials and leave the
(x^2+12x)+20
Now we take the 12x and divide it by 2 and square the number
b/2=b^2
12x/2+6x^2=36
Now we add it inside binomial bracket now making it a trinomial
(x^2+12x+36)+20
Now we have to cancel out the 36 by subtracting it
(x^2+12x+36-36)+20
Then we put the -36 with the +20
(x^2+12x+36)-36+20
Now we just solve the -36+20 and simplify the trinomial
(x^2+12x+36)-16
Simplify:
(x+6)^2-16
*Find the square root of the last term inside the trinomial and pay attention to the signs as well as if the number works to get the middle term for example the numbers 12 and 36 are positive you so you wouldn't have to worry in this case.
ex. √36=6
Thats how I got the number 6
*Also make sure that you expand the simplified equation to make sure that you did the steps correctly.
Check:
(x+6)^2
(x+6)(x+6)
x^2+6x+6x+36
x^2+12x+36
Word Problem Using Quadratic Formula
Define Variables:
Length=L
Width=(L-6)
Area= LxW
280=L(L-6)
280-280=L^2-6L-280
L^2-6L-280
ax^2+bx+c=0
L=b±√b^2-4(a)(c)/2(a)
L=-(-6)±√6^2-4(1)(-280)/2(1)
x=6±√36+1120/2
L=6±√1156/2
L=6+34/2
L=40/2
L=20
Now we the result of the discriminant and flip the operation so we change the plus into a minus:
L=6-34/2
L=-28/2
L=-14 NOT VALID
Now we check to see if its right:
Area=LxW
280=L(L-6)
280=(20)(20-6)
280=(20)(14)
280=280
Therefore the dimensions of the rectangle are 20 by 14 Metres.
My Video: Quadratic Formula & Completing The Square
Resources: Quadratic Formula
Completing The Square
Reflection
In addition
this was my first time approaching Quadratics and revisiting skills that I had learned in the past. For me to understand Quadratics I had to get extra help and do my Homework every night to keep up with the unit and get anall round
The first Part of Quadratics being Vertex Form I did not do so good,Then I started doing extra practice as well as extra help to clarify my mistakes and strengthen my weak spots. This then led me to
doing
good on my Factored Form then eventually I got a really good mark on my Standard Form unit test.For me, Vertex Form was the hardest and Standard Form was the easiest in the unit Quadratics. I think that Quadratics is a challenging unit because you have to know the different forms such as Vertex Form, Factored
Form
and Standard Form. Plus, you have to know how to apply the forms in word problems.Also
there's a lot of methods on how to solve the different equations whichis
good.In conclusion, these are my thoughts on the Grade 10 Math Unit Quadratics. Remember to the DAILY HOMEWORK and GET EXTRA HELP IF NEEDED! Extra Help always helps!
Assessments
Connections throughout Quadratics
Instead of using Completing the square to find the Vertex I could Use the Quadratic Formula to find the zeros then add the zeros and divide the result by two which gives me the Axis Of Symmetry. Once I find the Axis Of Symmetry I could sub the x value in the original equation which will give me the vertex.
For Factored form, you can expand to get standard form and vice versa
When graphing you can use the Completing the square to find out the vertex easily then graph the vertex or just use the Vertex Form and plot the graph.
All these forms are
dependant
on each other to solve for xand
y.
For example without the quadratic formula, you can't find the x-intercepts or the zeros.
These are the connections to the other forms in Quadratics.