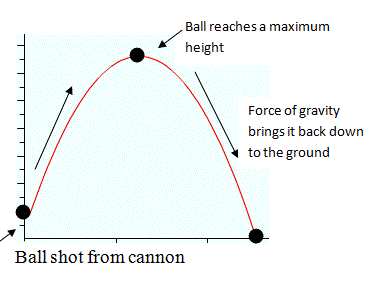
Quadratics
By: Kiranjit Aujla
Table of Contents
What is Quadratics?
- Quadratics
- How to identify Quadratic Relations
- Important Terminology
Vertex Form
- What is Vertex Form
- What the variables represent in Vertex Form
- The Different Transformations
- Graphing Vertex Form when not in Basic Form y=a(x-h)²+k
- Finding the Axis of Symmetry
- Finding the Optimal Value
- Finding the X-Intercepts/Zeros
- Finding the equation with one point and the vertex
Factored Form
- What is Factored Form
- Finding X-Intercepts/Zeros
- Finding Axis of Symmetry
- Finding the Optimal Value
- Graphing Factored Form
5 types of Factoring
- Expanding/Multiplying Binomials
- Common Factoring
- Factor by Grouping
- Simple Trinomials
- Complex Trinomials
- Perfect Squares
- Difference of Squares
- Graphing from Standard Form
- Word Problems
Quadratics 3
- Completing the Square
- Solve by Isolating X
- Quadratic Formula
- Discriminates
Reflecting on Quadratics Unit
- Assessment Reflection
- Quadratics Reflection
What is Quadratics?
Quadratics
The name comes from "quad" meaning square, because the variable gets squared. There are three different types of quadratic relations: vertex form, factored form and standard form.
A graphed quadratic realtion forms a parabola, which is a curved line. You may not notice but we see parabola's in our everyday life from roller coasters to rainbows.
How to identify Quadratic Relations
- Linear relations had first differences
Therefore:
- Quadratic relations have second difference
Important Terminology
- Vertex: the maximum or minimum point on the graph, the point where the graph changes direction (x,y)
- Minimum/Maximum Value: the highest or lowest point, the y value of the vertex or optimal value (y=#)
- Axis of Symmetry: the line that cuts the parabola in half, the x value of the vertex (x=#)
- Y-Intercept: where the parabola crosses the y-axis
- X-Intercept: where the parabola crosses the x-axis
- Zeros: the same thing as x-intercepts
Vertex Form
What is Vertex Form?
- The quadratic relation is written as y=a(x-h)²+k
- The basic form of it is y=x²
- An example is y=3(x-5)²+2
- The "x" and "y" are variables for this relations x and y intercept(s)
What the variables represent in Vertex Form
- in y=a(x+h)²+k (vertex form), each variable has a different part to contribute
- the "a" tells us if there is a stretch or compression to the parabola
- the "h" lets us know the axis of symmetry and the vertex's x value
- the "k" tells us the vertex's y value
The Different Transformations
- A parabola can transfer by a reflection in the x axis, vertical stretch/compression, a horizontal shift and a vertical shift
- the "a" value stretches or compresses the parabola, if the "a" value is larger than 1 it will be a stretch and if it is smaller than 1 it will be compression
- the "a" value being negative lets us know the parabola will have a reflection in the x-axis
- the "h" value affects the horizontal shift of the parabola, it moves opposite of its sign. If it is positive it moves to the left, if it is negative it moves to the right
- the "k" value affects the vertical shift of the parabola. If it is positive it will move up, if it is negative it will move down
Graphing Vertex Form using the Step Pattern
- The original step pattern is "over 1 up 1, over 2 up 2"
- This pattern can be used as long as the parabola is the basic one (y=x²)
Steps:
- First, graph the vertex
- Next, plot the following points by using the basic step pattern
Example:
y=(x-5)²+2--> is a basic parabola
To Graph:
Plot the Vertex: (5,2)
Then use the step pattern "over 1 up 1, over 2 up 2", to plot the other four points.
Graphing Vertex Form when not in the Basic Form {y=a(x-h)²+k}
- if the vertex form relation has a "a" value in it, it is not a basic parabola as it will either stretch or compress and/or make a reflection in the x-axis
- the changing of the step pattern depends on the value of "a"
Steps:
- First, graph the vertex
- Next, multiply the original step patterns vertical point by the "a" value (it does not matter if the "a" value is a decimal, fraction or a whole number the steps are the same)
- Then, plot the plots using the new step pattern
Example:
y=2(x-5)²+2--> not a basic parabola (has "a" value)
To Graph:
Plot the Vertex: (5,2)
Multiple the vertical point of the step pattern by 2 (the "a" value)
Step Pattern: over 1 up 2, over 2 up 8
Plot the other four points using the step pattern
Finding the Axis of Symmetry
- it is written as x=h, it is the "h" value in the equation
Example:
The axis of symmetry of the parabola above is x=4, as it is the vertical mid-line of the parabola and x intercept of the vertex.
Finding the Optimal Value
- it is written as y=k, it is the "k" value in the equation
Example:
The optimal value of the parabola above is y=-6, as it is also the y intercept of the vertex.
Finding the x-intercepts/zeros
- set the y=0 in the equation and solve for x
- also you could look at the graph and figure out the x-intercepts/zeros
Example:
y=-4(x+3)²+20
0=-4(x+3)²+20
-20=-4(x+3)²
-4 -4
+√5=(x+3)²
Therefore 4 and -4 will be placed for y and then solved for x
4=x+3
4-3=x
1=x
-4=x+3
-4-3=x
-7=x
X-Intercepts: (1,0) and/or (-7,0)
- the square roots are negative and positive because the number being squared could be either
Questions with Solutions
Word Problem Example
Finding the equation with one point and the vertex
- first write the equation using the vertex (substitute the vertex point for the "h" and "k" variable in the equation)
- second, plug in the x and y point values for the "x" and "y" in the equation
- solve for "a"
Example Question
Factored Form
What is Factored Form?
- the quadratic relation is written as y=(x-r)(x-s)
- an example is y=0.5(x+4)(x-1)
Finding x-intercepts and zeros
- can be determined by setting each factor equal to zero (x-r=0 and x-s=0)
- for example, using the equation above the zeros would be found by making (x+4) and (x-1) equal to zero
x+4=0
x=-4+0
x=-4
x-1=0
x=1+0
x=1
X-Intercepts: (-4,0) and (1,0)
Finding Axis of Symmetry
- can be found by adding the two x-intercepts and dividing it by two
- the formula is x=(r+s)/2
- for example, using the equation we have been using the axis of symmetry for it would be:
x=(-4+1)/2
x=(-3)/2
x=-1.5
Axis of Symmetry: x=-1.5
Finding the Optimal Value
- can be found by substituting the axis of symmetry into the equation as the "x", as it is a x value on the parabola
- for example, the same equation used so far we would substitute x=-1.5 as the "x" in the equation y=0.5(x+4)(x-1)
y=0.5(x+4)(x-1)
y=0.5(-1.5+4)(-1.5-1)
y=0.5(2.5)(-2.5)
y=0.5(-6.25)
y=-3.1
Optimal Value: y=-3.1
Try this Question
Graphing Factored Form
- Plot the first x-intercept
- Plot the second x-intercept
- Plot the vertex (axis of symmetry and optimal value)
Example:
To graph the equation we have been using y=0.5(x+4)(x-1):
-First, we would plot the first x-intercept x=-4
-Then, we would plot the second x-intercept x=1
-Finally, the vertex would be plotted which is (-1.5,-3.1)
Check Your Understanding!
X-Intercept Word Problem
Types of factoring
Expanding Binomials
1. Multiply the number outside the bracket by all the numbers inside the bracket
Ex. 2(3-x)
=6-2x
-multiply the 2 by 3
-multiply the 2 by x
Multiplying Bionomials
2. Multiply the second number in the first bracket by everything in the second bracket
- If there is a number outside of the brackets, multiply it by everything in side the bracket like you usually would {ex. 5(x+5}
- if there is a power that means you multiply the binomial that many times by its self {ex. (x+5)²-->(x+5)(x+5)
(x-2)(x-5)
=x²-5x-2x+10
=x²-7x+10
Common Factoring
- Find the Greatest Common Factor (GCF)
- Divide the expression by GCF
- The GCF number will go outside the brackets
Example
Factor: xy-5y-2x+10
=(xy-5y)(-2x+10) [group the terms that have common factors together and factor]
=y(x-5)-2(x-5) [identify a common factor between both terms]
=(x-5)(y-2) [factor]
Another Example
Factor by grouping
Steps:
- Identify two terms the are common
- Group each pair of common factors with brackets around them (usually the first two terms and the second two terms)
- Factor as you usually would
- Identify the common factor
- Now factor again
Factoring Simple Trinomials
- written as x²+bx+c
- the coefficient in front of x² is one for simple trinomials
Steps:
- Make sure that the format is x²+bx+c
- Write down all factors of the "c" value
- Identify which factor pair adds up to the sum of the "b" value
- Substitute that factor pair into two bionomials (x+#)(x+#)
Example
Factors of 4 ("c" value) & their sum:
- 1x4 1+4=5
- -1x-4 -1+-4=-5
- 2x2 2+2=4
- -2x-2 -2+-2=-4
Therefore, 1x4 is the factor which's sum is 5 & a factor of 4.
Final Answer: (x+4)(x+1)
Factoring Complex Trinomials
- include an "a" value
- ex. 2x²+5x+6
Steps:
- List the factors of "c" which multiplied equal to the "c" value and when added equal to the "b" value.
- Guess and check which factors work by plugging them into factored form and expanding
- The first term in both brackets must equal to the "ax²" value when multiplied
Factoring Perfect Squares
- they make expanding easier
- there first and last term are square roots
- only if relation you are expanding is in the format (a+b)² or (a+b)(a+b) or (a-b)² or (a-b)(a-b)
Steps:
- Square the first term
- Double Product
- Square the second term
Communication Problem
Factoring difference of squares
- not a perfect square
- is in the form of (a-b)
Steps:
- Square the first term
- Square the second term
IMPORTANT: difference of square factors into a product of sum and difference.
Example
- y² square root=y
- 25 square root=5
(y+5)(y-5)
(can check by expanding)
Graphing from standard form
- Convert to Factored Form
- Substitute zero as y and find the x-intercepts
- Find the vertex by finding the axis of symmetry and optimal value (Axis of Symmetry: add the two x-intercepts and divide by two, Optimal Value: substitute the axis of symmetry as x and solve for y)
- Plot the vertex and two x-intercepts
Example
Word Problems
Motion Problems
Area Problems
Revenue Problems
Revenue Question
Revenue Answer
Quadratics 3
Completing the Square
- to convert from standard from y=ax²+bx+c to vertex form y=a(x-h)+k
Steps:
- take the "c" out and make it as the "k", put brackets around the two remaining terms
- factor out the coefficient of ax² (the "a" value)
- divide "b" by 2 and square it, then add and subtract it to "b"
- perfect square the first three terms in the bracket
- the subtraction number which is left after perfect square, multiply it by the "a" value
- simplify
Example
Solve by Isolating X
- set y=0
- move the "k" value to the other side (by adding or subtracting both sides by it)
- divide both sides by the "a" value
- square root both sides
- move the "h" value to the other side & put it in front (by adding or subtracting it)
Quadratic Formula
- to use the quadratic formula the standard form should equal to zero, since you are solving for the x-intercepts
- if it does not then re-arrange the standard form equation to make it equal to zero
Steps:
- Identify your "a", "b" and "c" values
- Substitute the values into the equation
- Solve
Example
- The square root is both positive and negative because there would be a negative a positive square root to the number which in the end would give us the two zeroes
Discriminants
- Discriminants is the number inside the square root (b²-4ac) of the quadratic formula
- it helps you tell how many x-intercepts a quadratic equation has
Steps:
- Subsitute the values of "a", "b" and "c" from your equation into the quadratic formula
- Solve for the discriminant but do not square root it
Therefore...
- If the discriminant is less than 0, there are no x-intercepts
- If the discriminant is larger than 0, there are two x-intercepts
- If the discriminant is 0, there is one x-intercept
*Discriminants and zeros are the same thing
Reflecting on Quadratics Unit
Assessment: Quadratics 1 Mini Test
Quadratics Reflection
The quadratics unit overall has taught me many new things that I will use in my life and has been a time consuming unit in which I gathered a lot of methods and formulas. I learned quadratics is all around us such as rainbows, in logos, mountains and bridges. First off, I learned about the different types of quadratic equations standard form, vertex form and factored form. To understand the different types was very difficult for me at first, but later on the unit I understood it very well. I could see the connections between the different types and also learned how to convert from one to another. Next, I would always get confused with complex trinomials because I would use the same method as simple trinomials. But with more practice and clarification I soon realized the difference and understood why the same method would not work. Graphing from vertex form was one concept I found easy and learned quick. I thought the step pattern was very easy to understand. Sometimes converting from standard form to factored form was difficult as there are many steps. But, understanding why each step occurs really benefited me and I started making less mistakes. Learning about the values in all of the equations and what change they make to that equation, answered many of my questions. This also let me create my own problems and check if they would work. I also figured out that we can find the height of a parabola or a building using quadratics. Also, sometimes doing homework on the same topic over and over again was very annoying, but all of that practice improved my skills at the end. During quadratics I hardly got lost, but when I did I would always ask for help. Understanding the concepts such as difference of squares and perfect squares was sometimes hard, but practice made it all better. Quadratics is a complex unit, but completing your homework and staying on top of things helps successfully understand it. It consists of many different concepts and at the end you learn how they all connect. Quadratics was a very interesting and fun unit. All and all, quadratics was a very fun and interesting unit.