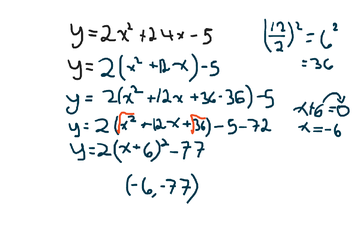Quadratics
Standard Form
Learning Goals
2)What is a standard form equation?
3)How do you complete the square?
4)How do you word problems using the completing the square/quadratic formula?
5)What is discriminant?
Standard Form: ax^2+bx+c
Quadratic Formula
- The reason for using the quadratic formula, is to find the x-intercepts of standard form equation.
- This makes graphing a parabola easier
- To find the x-intercepts of an equation, you must sub that equation into the quadratic formula.
- Once you sub the numbers in, you can easily find the x-intercepts by looking at what the equation leads you to.
Ex: y=3x^2-8x+2
x=-(-8)+/-\(-8^2-4(3)(2))/2(3)
x=8+/-\(64-24)/6
x=8+/-6.3
x=2.4
x=0.3
Complete The Square
- y=ax^2+bx+c--->y=a(x-h)^2+k
- The reason for completing the square is the find the vertex of a standard form equation
- When completing the square, you are converting a standard form equation to a vertex form equation
- This makes graphing a parabola easier
- To complete the square, you must factor the first 2 terms of a standard form equation
- Then you must divide the 'b' value by 2, then square that value
- Make sure that the value that you get is positive and negative
- Take the negative value out of the brackets, then multiply it with the number that factored the first 2 terms of a standard form equation
- Square root the first and the last values that are inside that bracket
- Add of subtract the terms that are outside of the brackets
- Put the numbers that are square rooted in a bracket, make sure that the bracket is squared.
Ex: y=2x^2+24-5
y=2(x^2+12x)-5
y=2(x^2+12x+36-36)-5
y=2(x^2+12x+36)-5-72
y=2(x+6)^2-77
Word Problem Using Quadratic Formula
Let x rep unknown dimensions
(x)(x-6)=280
I did this because I know that the width will be 6m less that its length, so i kept the length as x and the width as x-6, i am choosing to multiply them together because length times width is the area of a rectangle which in this case is 280m^2
x^2-6x=280
=x^2-6x-280
I brought the 280 to the other side because I wanted to make a a standard form equation to find my length
x=-(-6)=/-\(-6^2-4(1)(280))/2(1)
x=20
I used the quadratic formula to solve for x which is supposed to be my length, i did not subtract because I know that my length has to have a positive value.
(20)(20-6)=280
(20)(14)=280
Therefore the length of the rectangle is 20m, and the width of the rectangle is 14m
Word Problem Using Complete The Square
Let y rep revenue
Let x rep increases and decreases in money
Let p rep price
y=(12-0.5x)(36+2x)
y=-x^2+6x+432
y=-(x^2-6x)+432
y=-(x^2-6x+9-9)+432
y=-(x^2-6x+9)+432+9
y=-(x-3)^2+441
p=12-0.5(3)
p=12-1.5
p=10.5
Therefore, Mrs. Marshall can maximize her revenue at $10.50
Discriminant
- The discriminant is the final value that is in the square root part of the quadratic formula.
- If the value of the discriminant is positive and greater than 0, the parabola will have 2 x-intercepts.
- If the value of the discriminant is negative, the parabola will have no x-intercepts.
- If the discriminant has a value of 0, the parabola will have 1 x-intercept.
Ex: \(25)
The discriminant is positive and greater than 0, therefore the parabola will have 2 x-intercepts
Ex 2: \(-30)
The discriminant is negative, therefore the parabola will have no x-intercepts
Ex 3: \(0)
The discriminant is 0, therefore the parabola will have 1 x-intercept
Graphing
Summary of Unit
Reflection
- To end off, I believe that the course of quadratics was very interesting and fun to work with.
- Though Quadratics got confusing at times, it was a great learning experience that will surely lead me to a bright and successful future.
- The course of quadratics is based on graphing lines that are non-linear, also known as quadratic
- Quadratic relations have an exponent of 2 placed in its equation all of the times (unless factored form)
- Quadratics is a very useful unit, which will be effective for our futures
Assessment
- This is an application question that I received on my Quadratics Standard Form test. I chose this exact question as an assessment that I would share because I struggled a lot with this type of question in the past, and finally, after large amounts of practice, I was able to answer this question, and receive full marks on my test for it.
- This connects to expansion in the quadratics units, as I expanded my equation. This also connects to the quadratic formula, as I used the formula to find out the length of the rectangle.
Connections
This is because when factoring a standard form equation, you are able to find the x-intercepts of the parabola which will get you one step closer to graphing the equation
Vertex Form connects to graphing:
This is because when you complete the square of a standard form equation, you are able to find the vertex of the parabola, this will give you an advantage when graphing, as you know the highest or lowest point in the graph.
Factored form connects to standard form:
This is because, a factored form equation is practically the standard form (nothing changes) however now you have the x-intercepts. They also connect as you can get from factored for to standard form by expanding the equation
Ex: a(x-r)(x-s)--->ax^2+bx+c
You can also get from standard form to factored for by factoring the equation
Ex: ax^2+bx+c--->a(x-r)(x-s)