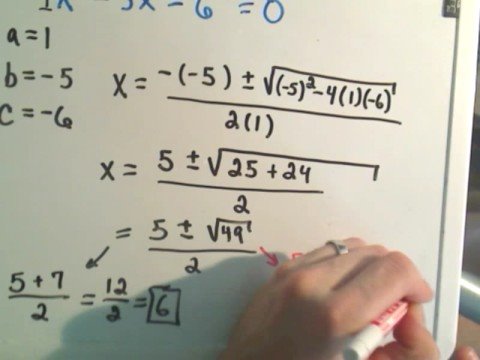Solving A Quadratic Relationship
WHERE LINES INTERSECT
Overveiw of the Unit
In this unit we learned how to graph parabolas and find the intersection points in any of the 3 forms the parabolas might be in. We learned to graph:
- Vertex Form
- Factored Form
- Standard Form
Terminologies what you need to know
1. X intercepts- where the graph intersects the x axis making the y coordinate 0.
2. Y intercepts- where the graph intersects the y axis making the x coordinate 0. 3. Optimal Value- the y value of the vertex and also the highest/ lowest point on the graph. 4. Axis of Symmetry- where the parabola gets divided into 2 halves (x-axis). 5. Zeros/ Roots- the x value the makes the y value zero. 6. Vertex- the point where the axis of symmetry and optimal value intersect.
Linear Relationship or Quadratic Relationship or None
We learned to tell the differences from quadratic relation and a linear relationship by just writing out the x and y coordinates into a graph shown below. It gives an idea to students of how the graph will eventually turn out.
Fireball Experiment BBC
The first parabola problem we encountered in this unit, we learned the definitions of the points and factors the make up a quadratic relation. Zeros, x intercept, y intercept, optimal value and axis of symmetry.
Graphing in Vertex Form (y=a{x-h}+k)
We learned to graph vertex form, the easiest of all 3 forms, by learning what "k", "a" and "h" meant. The vertex consisted of k and h, where k was the y coordinate and h the x coordinate. And "a" was simply the stretch factor in the equation. We also learned the terms horizontally translated, vertically translated, vertically stretched and vertically compressed etc..
Graphing from Factored Form
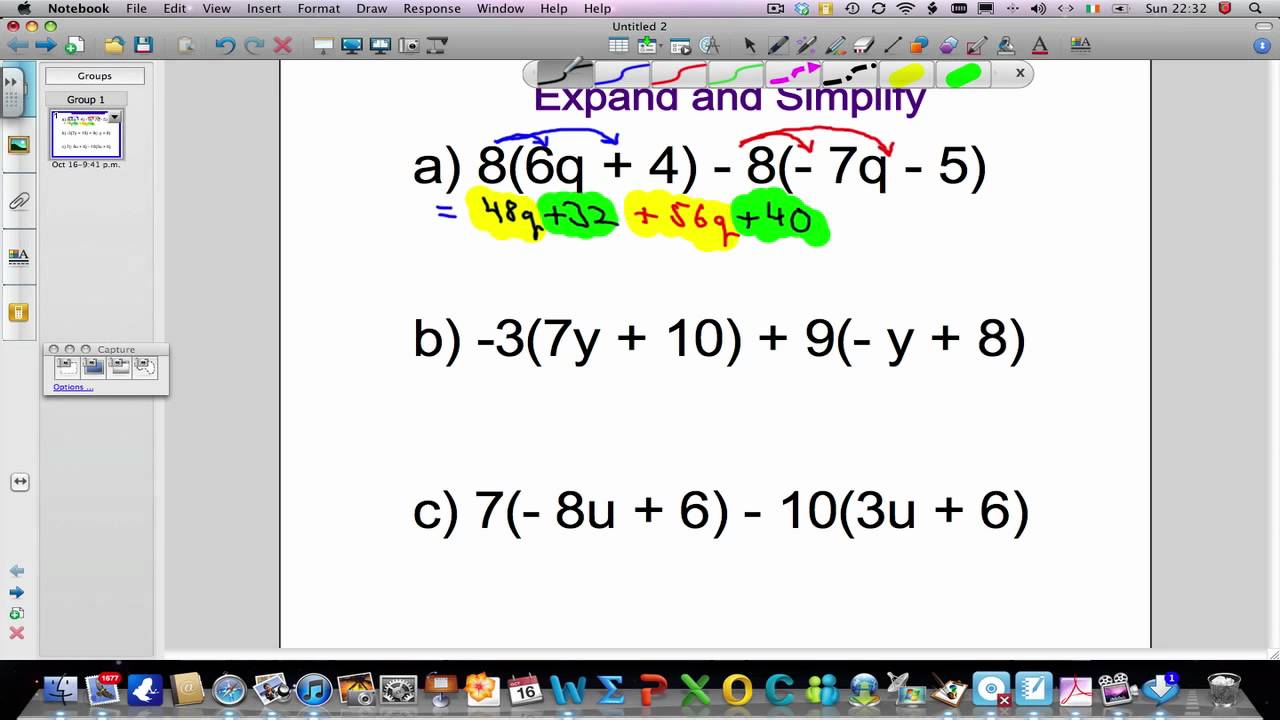
We learned to graph factored form after learning to graph vertex form. Factored form is not the worst state to have a quadratic equation in and it certainly isn't the best state. It's the second option if you don't don't have vertex form. "Expanding and Simplifying" is a method used to covert factored form into standard form. Factored Form is commonly used in optimization problems and getting the zeros.
Finding x intercepts
Expanding and Simplyfing
Graph of a factored form equation
Common Factoring
We learned to common factor which basically means taking out anything common in the polynomial and bringing it outside the brackets. Common factoring applies to polynomial and not trinomials.
Factoring Simple Trinomials
Simple Trinomials are usually in standard form and factoring them converts them to standard to factored form. Trinomials unlike Polynomials have 3 parts to the equation.
Trinomials how to factor standard to factored form
Step by to factor and convert
Graphing Standard Form
Standard form is the worst form to have an equation in. It gives the least information on how to graph, and that why we convert standard to vertex form or factored by completing the square and factoring.
Completing the Square
A method used to convert standard form to vertex form which is very useful when graphing standard form. We learned this method later in the unit.
Quadratic Formula
A method used to find the x-intercepts/solutions when factoring gets to messy. A formula that is helpful.
Reflection
The unit of quadratics taught me many forms to solve a problem in a real world situation. In the first part of the unit, we learned to vertex form and how to graph and what optimal value. AOS, and step pattern meant. In part two learned what factored form and standard form was and how to graph it. We to factor equations. In the last part of the unit, we learned about the quadratic formula, -b/2a and completing the square. This unit showed me ways on how I can solve problems that I couldn't answer in the past. The first unit was very simple and easy, and I had no problems on the the first test. The second part of the unit was ok and I did fairly well and the last part f the unit was child's play. Overall this unit was quite the most useful one that Ii took for a count.