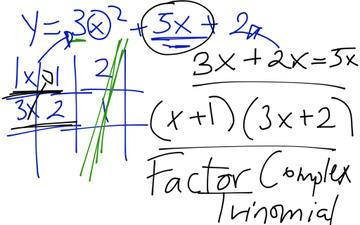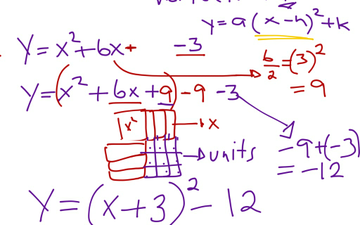Quadratic Unit Assignment
By:Tharakaa Rajakumar
Definition Of Quadratics:
Table Of Contents
Introduction
1. Quadratic Relations- Second differences
2. Introduction To Parabola
- Parabola's Labels
- The Parabolic Definitions
3. Transformations Of Quadratics
- The Base
- The Step Pattern
Types Of Equations
1. Factored Form- Expanding/Distributive Property to Standard Form
- Difference of Squares
- Perfect Squares
- Graphing Factored Form
- Common Factoring
- Factoring Simple Trinomials to Standard Form
2. Standard Form
- Completing The Square Standard Form To Vertex Form
- Grouping Standard form to Factored form
- Complex trinomials standard form to factored form
- Quadratic Formula
- Discriminant
3. Vertex Form
- Graphing Vertex Form
- Solving For X
- Solving For Y
Word Problems
- Optimization questions
Connection To All The Quadratic Parts and Reflection
Types of Quadratic Equations
2. Factored Form: y=a(x-r) (x-s)
3. Standard Form: y=ax² + bx + c
Quadratic Relations Using Second Differences
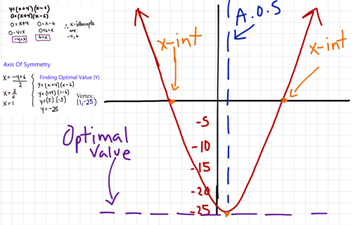
Defintion of Parabolic Terms
2. Axis of Symmetry- Is the line that divides the parabola into two symmetric portions
3. X-intercepts- Points on the graph that intercept the x-axis.
4. Y-intercepts- Points on the graph that intercept the y-axis
5. Optimal Value- Highest y-value of a parabola.
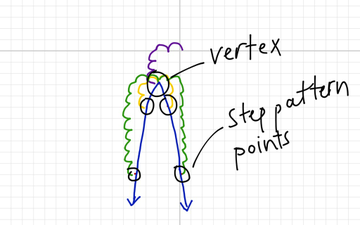
The Step Pattern
The Transformations
Factored Form
Expanding/ Distributive Property
There are two ways to do Expanding In Factored Form to Standard Form in distributive property.
1. Simple distributive property is used when there's only a variable like x with no coefficients in front
2. FOIL in expanding for when there is a coefficient beside the variable x.
F- First
O-Outer
I-Inner
L-Last
Ex.1 (6x +1) (x-3)
F- (6x) (x) = 6x²
O- (6x) (-3)= -18x
I- (1) (x) = x
L-(1) (-3) =-3
= 6x² -17x-3
Perfect Squares
Perfect Square Algebra Tiles
Perfect Square Algebra Tiles
How to factor a perfect square
Difference Of Squares
a² - b² or (9x+8y) (9x-8y)
= 81x² - 72xy + 72xy - 64y²
= 81x² - 64y²
The (9x) multiplies with the other (9x) which becomes (81) and then the two (x's) square and as a total becoming (81x²). Then the (9x) multiplies with the (-8y) which equals to becomes (-72xy). Now, multiply the (8y) with the (9x) which equal to becomes (72xy). Lastly (8y) multiplies with (-8y) equalling to (-64y²)
Overall the standard form would look like this:
81x² - 64y²
How To Graph Factored Form
Or click on the embedded link below.
Standard Form
How to Factor Complex Trinomials #1
Or click on the embedded link below.
How to Factor Complex Trinomials #2
This is another one of my videos that i made for Factoring Complex Trinomials
https://www.educreations.com/lesson/view/how-to-factor-complex-trinomials/27575797/?ref=link&s=aAHitkOr click on the embedded link below.
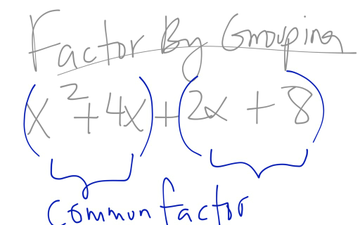
Factoring By Grouping
This is my own video on how to factor with grouping.
https://www.educreations.com/lesson/view/grouping-final/27576038/?s=EqkFMm&ref=appemailOr click on the embedded link below.
How To Use The Quadratic Formula
Discriminant
Common Factoring
Example 1: 2x² + 8
Common factor between 2x² + 8x is:
2x² - (2) (x) (x)
8x - (2) (4) (x)
The common factors in this equation is: (2) (x)
So you put the 2x in front and then put a bracket and then divide 2x² with 2x... and 2 is left and then you divide 8x with 2.....and 4 is left
This is how the answer will look like:
2x(x+4)
This is common Factoring
Completing The Square
This is my own video on completing the squares
https://www.educreations.com/lesson/view/completing-the-square/27617938/?ref=link&s=MwtnC0
Or click on the embedded link below.
How To Graph Vertex Form
Or click on the embedded link below.
Word Problems
Connections
They all used the graphing method by find the x-intercepts to find the vertex. The Standard form looked like: y=ax² + bx + c. You could use standard form to answer word problems like to find the maximum height or when the ball will hit the ground it etc. It is also used to for Quadratic Formula when as the middle value is b and the last value is c and the first value is a. Secondly Factored form looks like: y=a(x-r) (x-s). This formula is used for factoring all types like Simple and complex trinomials and etc. Lastly, Vertex form looks like: y=a(x-h)² + k. This formula is used for perfect squares and many more. But mostly these forms relate to the graphing because these forms are just showing different ways you can do to graph. Like Factored form finds two x-intercepts to graph and so does quadratic formula these forms relate to our understanding to make life easier. So whenever there is a hard question we use the easiest way to answer the question instead of the long way. For example, Quadratic Formula and Factored Form both solving for x. Depending on the form and the question you use either one applicable.