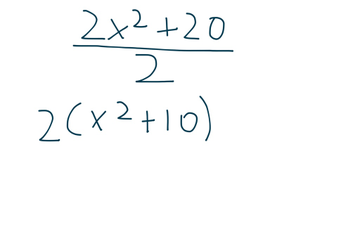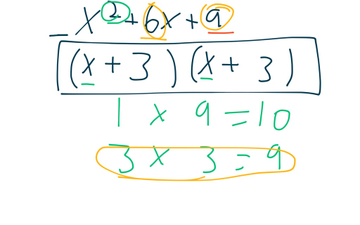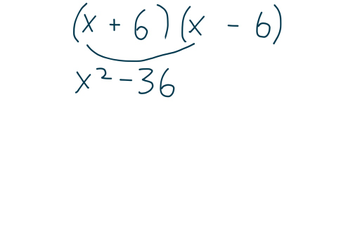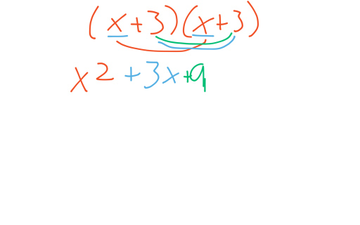Grade 10 Quadratics
BY: Karman Gakhal
Table of contents
Introduction picture
1. Expanding and Simplifying
- Factoring Standard Form
- Common Factoring
- Factoring by Grouping
- Simple Trinomials
- Complex Trinomials
- Difference of Squares
- Perfect Squares
- Completing the Square
2. Graphing
-Standard Form
- x Intercepts
- Axis of Symmetry
- Each Part of Equation
- Types of Graphs
- Transformations
- How to Graphs
- x Intercepts
- Axis of Symmetry
- Optimal Value
3. Standard form
- Learning Goals
- Summary
- Quadratic Formula
- Completing the Square
- Word Problem
4. Solving
- Solving Standard Form
- Solving Vertex Form
- Solving Factored Form
5. Word Problems
6. Reflection
7. Connections
8. Useful links
What is a parabola?
Solving: Expand and Simplify
Factoring Standard Form
Learning Goals
how to factor by grouping
How to factor simple trinomials
How to factor complex trinomials
How to find the difference of squares
How to find factor perfect squares
Basic formula for factoring
Summary
The value of a gives you the shape and direction of opening
The value of r and s give you the x-intercepts
Axis of symmetry, AOS: 𝑥 = ( 𝑟+𝑠 2 ) Sub this x value into equation to find the optimal value To find the y-intercept, set x=0 and solve for y
Solve using the factors
Types of Factoring:
Greatest Common Factor
Simple factoring (a=1)
Complex factoring
Special case - Difference of squares
Special case – Perfect square
Common Factoring
Video
Factoring by Grouping
Simple Trinomials
Video
Complexed Trinomials
Video
Deference of Squares
Video
Perfect Squares
Video
Completing the Square
Word Problem
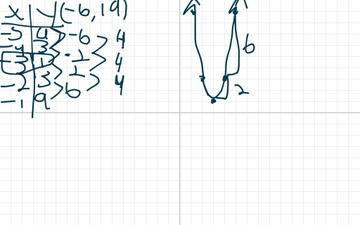
1)Write the formula in factored form
h=-2(t-6)(t+4)
2)When will the ball hit the ground
6 seconds (t=6)
3)What is the maximum height the ball will reach in metres?
50m
Graphing
Standard Form
Vertex Form
Learning Goals
2. How to graph vertex form
3. Equation for vertex form
4. Variables in vertex form
5. What a standard graph looks like
6. How to make a standard graph match your parabola
7. First and Second difference
8. Step Pattern Method
Each Part of Equation
H= tells us how many units left/right the vertex is going to move from 0
K= tells us how many units up/down the vertex is going to move from 0
X= the the 'y' are coordinates on the graph
Transformations
Math has its own language and there is specific terminology that you must know. When explaining the transformations of certain coordinates of a vertex form graph, there are certain words we use. These words are:
- Vertical Stretch: If the 'a' is a number greater than 1 then the graph would have a vertical stretch which means that is steeper. The way you would write it: This graph has been vertically stretched by the factor of 2 (or any number greater than 1).
- Vertical Compression: If the 'a' is a number less than 1 then the graph would have a vertical compression meaning it would be wider. The way you would write it: This graph is vertically compressed by the factor of 0.5 (or any number less that 1).
- Vertical Reflection: If the 'a' is a negative number then it means the graph is vertically reflected over the x axis downwards.
- Translations: If there is a number after x squared like in y=a(x-h)²+5 (the 'h') then it means that the vertex has been translated right or left. The way you would write it: The vertex has been horizontally been translated 3 (or any other number) units to the right/left. Also if there is a 'k' then that means that the vertex has been translated up or down. The way you would write it: The graph has been vertically translated 4 (or any other number) units up/down.
Step patterns (Basic)
Over 1 -- Up 1
Over 2 -- Up 4
Types of Graphs
maximum
minimum
2 X-intercepts
1 x-intercept
no x-intercept
How to Graphs
solving
Solving Standard Form
Quadratic Formula
Discriminant
X-Intercepts
Solving Vertex Form
Y-Intercept
X-Intercept part 1
X-Intercept part 2
Factored Form
Factored Form
Zeros & Axis of Symmetry
Optimal Value
Standard Form
Learning Goals
- What is the quadratic formula used for
- what is the quadratic formula
- how to complete squares
Summary
Quadratic Formula
Completing the Square
Word Problems
flight
A ball is thrown upwards at an initial velocity of 8.4m/s, from a height of 1.2 m above the ground. The height of the ball, in meters, above the ground after t seconds is modeled by the equation h=-4.9t²+8.4t +1.2.
1. How long will it take for the ball to fall to the ground, rounded to the nearest tenth of a second?
2.What is the maximum height of the ball? At what time will it reach this height? Round your answers to the nearest tenth.
Factor Quadratic Expressions
The flight of a ball is modeled by the equation ℎ = −5² + 20 + 25 where h represents the height of the ball in meters, and t represents the amount of time the ball has spent in the air in seconds.
a. Write the equation in factored form, determine the x-intercepts and vertex, and graph.
b. When does the ball hit the ground?
c. What is the highest the ball flies, and when does that happen?
Reflection
connections
In quadratics 1, we mostly focused on solving vertex form by finding axis of symmetry, optimal value, zeros, and determining the step pattern. With all this information, we were able to graph it.
In quadratics 2, we focused on expanding and factoring. We learnt how to find axis of symmetry, optimal value, and zeros. We also did this in quadratics 1, but the only difference was that there might have been some different methods to do this.
In quadratics 3, we focused on rewriting standard form equations into vertex form by completing the square and by learning a new equation which is called the Quadratic Formula. We also learnt how to graph quadratics using the x-intercepts which we also learnt in quadratics 1.
In quadratics 1, 2 & 3, the word problems were mostly all asking for the same stuff just in different forms of equations and different methods of asking them. For example, what is the max height? They are asking for you to find the vertex and state the 'y'. In vertex form {y=a(x-h)²+k}, the vertex is (h,k) and so you already know your max height by just looking at the equation and knowing 'k' is your 'y-intercept'. In standard form {y=ax²+bx+c}, you know that the 'c' is the 'y-intercept' which is your max height. Now in factored form, you have to do some solving to find the max height, starting with finding the zeros, then the AOS, & lastly the optimal value. The AOS and optimal value would be your vertex, at which the optimal value is the 'y-intercept'.
As you can see, all of the parts of quadratics are related in several ways.