Five Practices
for Orchestrating Productive Mathematics Discussions
Learning Goal
We are learning to facilitate productive class discussions based on rich student learning tasks
- Establish mathematics goals to focus learning
- Implement tasks that promote reasoning and problem solving
- Use and connect mathematical representations
- Facilitate meaningful mathematical discourse
- Pose purposeful questions
- Build procedural fluency from conceptual understanding
- Support productive struggle in learning mathematics
- Elicit and use evidence of student thinking
Facilitating Meaningful Mathematical Discourse
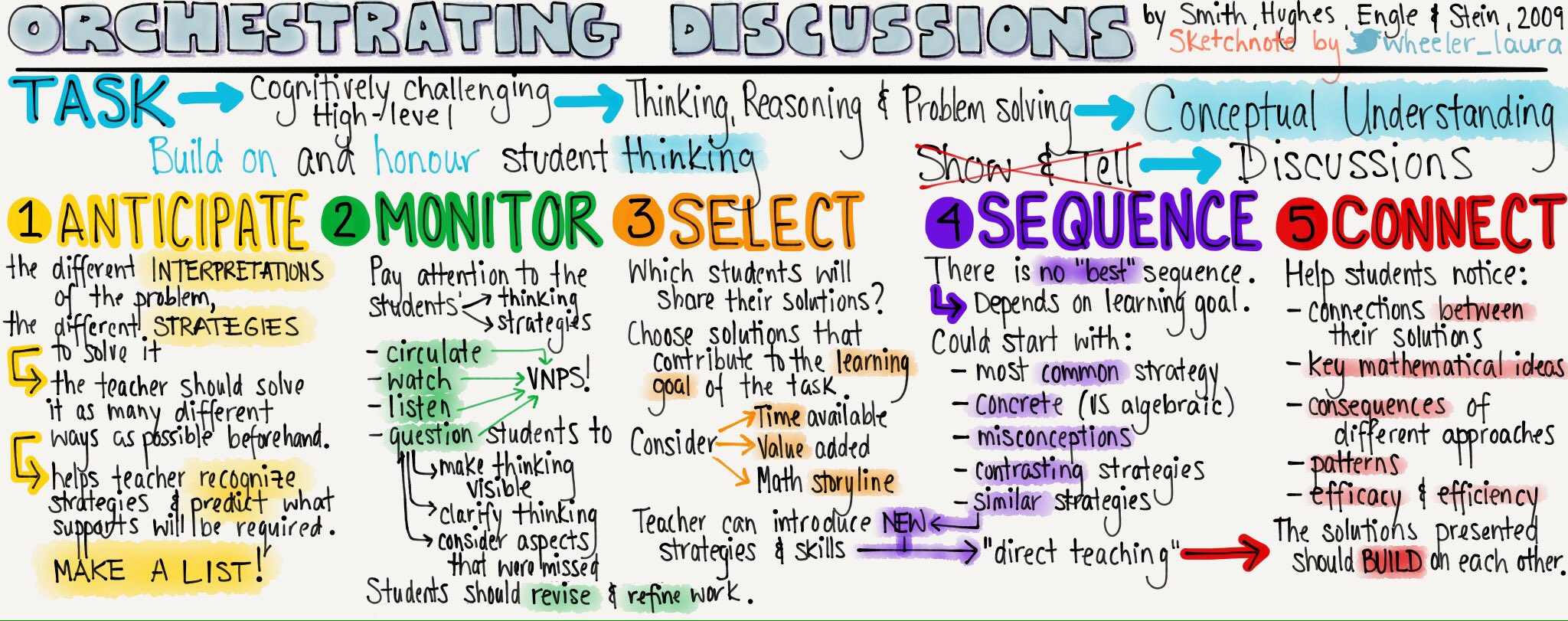
Anticipate
Brainstorm the approaches that students might use as they work on the task, considering both correct and incorrect ideas.
Teachers might work individually or collaboratively to anticipate solutions
Research may be useful to identify common misconceptions (e.g. Marian Small)
Teachers can analyze samples of student work from previous years
Consider what actions you will take when a student uses a particular approach. For example, what questions will be asked to elicit student thinking? How can you move the student's thinking forward without giving away the solution to the problem?
Monitor
Keep an eye out for other approaches that might be highlighted during the whole class discussion, especially those that were unanticipated. You may not choose to use an unanticipated approach in the consolidation, but make sure to add it to your lesson notes for next time.
Ask Assessing Questions that make student thinking visible. Make sure you stick around to hear the answer!
Ask Advancing Questions that challenge students to revise strategies or consider other aspects of the task (which may have been neglected). Ask an advancing question, then leave. Show students that you have the confidence in their ability to work through your advancing question on their own rather than needing you to be nearby as they expand their thinking. Come back later to see what they have done.
Remember, EVERY student deserves an assessing question and an advancing question.
Select
Decide which student solutions will be used to consolidate the mathematical learning goal. Not all student solutions will be selected. This allows the teacher to orchestrate a focused discussion leading to a deeper mathematical understanding.
You may inform selected students (or groups of students) that they will be asked to discuss work of you might use a combination of volunteers and strategically selected students.
Strategically selected students fall into one of two categories.
Students who were in a different group but followed a similar strategy.
Students who have shown evidence of interesting insights and useful ideas that will help move the class towards the mathematical learning goal.
Sequence
The student work selected should offer different representations and solution paths.
There are many approaches for sequencing the work, each with different benefits. Some examples include
- Share the most common strategy first
- Progress from concrete to abstract (it is ok if some of the shared work is not complete)
- Address common misconceptions first
- Share a unique approach first or last
There is no 'one best way' to sequence work. Rather, teachers should consider the learning goal and their students when deciding what order they will present the work.
Connect
It is important to focus on building two types of connections:
Between a students' own solution and the other solutions
To the key mathematical idea
Rich Tasks Discussion Tool
Creating great discussions deepens heavily on the implementation of a worthwhile task. Tasks must promote deep enough reasoning and problem solving so that they can provoke a rich conversation.
- Mathematical Focus
- Connections to prior knowledge
- Opportunities for problem solving
- High cognitive demand
- Opportunities to use multiple tools and/or representations
- Multiple entry points
- Intellectual or social engagement
An eighth possible category could be opportunities for making effective use of technology.
Orchestrating Discussions
Five Practices for Orchestrating Productive Mathematics Discussions
Principles to Actions
Blooms Taxonomy Teacher Planning Kit
Along with many question prompts to support each level of thinking in Bloom's Taxonomy, the planning kit also provides examples of keywords that align to the different levels, actions students might be involved in, and outcomes they might be asked to produce.
Teacher Monitoring Tool
Task From the Session (And others we have used)
The Field Problem
On the map he has the property measures 2 cm by 5.8 cm. He needs to calculate the dimensions of the actual property, but doesn't know how to start.
Explain how to find the dimensions of the property.
A set of possible solutions for this problem created by educators at a Winter SIM session in 2014 was also used during our session.
Claudio Attanasio
Cardinal Ambrozic Secondary School
DPCDSB
Email: claudio.attanasio@dpcdsb.org
Mark Bouwmeester
DPCDSB
Email: mark.bouwmeester@dpcdsb.org
Twitter: @mrBouwmeester_